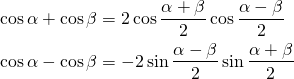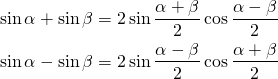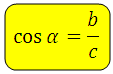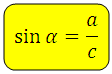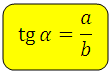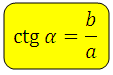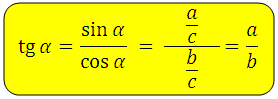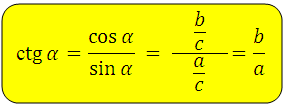Я не буду переконувати вас не писати шпаргалки. Пишіть! у тому числі, і шпаргалки по тригонометрії. Пізніше я планую пояснити, навіщо потрібні шпаргалки і чим шпаргалки корисні. А тут-інформація, як не вчити, але запам’ятати деякі тригонометричні формули. Отже-тригонометрія без шпаргалки!використовуємо асоціації для запам’ятовування.
1. Формули додавання:
Косинуси завжди «ходять парами»: косинус-косинус, синус-синус. і ще: косинуси — «неадекватні». Їм » все не так«, тому вони знаки змінюють: » — « на»+», і навпаки.
Синуси « «змішуються»: синус-косинус, косинус-синус.
2. Формули суми і різниці:
Косинуси завжди «ходять парами». склавши два косинуса -» колобка«, отримуємо пару косинусів — »колобків». А віднімаючи, колобків точно не отримаємо. Отримуємо пару синусів. Ще й з мінусом попереду.
Синуси — » змішуються» :
3. Формули перетворення твору в суму і різницю.
Коли ми отримуємо пару косинусів? коли складаємо косинуси. Тому
Коли ми отримуємо пару синусів? при відніманні косинусів. Звідси:
«змішання » отримуємо як при додаванні, так і при відніманні синусів. Що приємніше: складати або віднімати? правильно, складати. І для формули беруть додавання:
У першій і в третій формулі в дужках — сума. Від перестановки місць доданків сума не змінюється. Принциповий порядок тільки для другої формули. Але, щоб не плутатися, для простоти запам’ятовування ми у всіх трьох формулах в перших дужках беремо різницю
А по — друге-суму
Шпаргалки в кишені дають спокій: якщо забув формулу, можна списати. А дають впевненість: якщо скористатися шпаргалкою не вдасться, формули можна легко згадати.
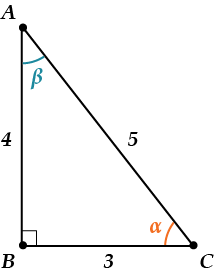
Де були розглянуті завдання на вирішення прямокутного трикутника, я пообіцяв викласти прийом запам’ятовування визначень синуса і косинуса. Використовуючи його, ви завжди швидко згадайте – який катет відноситься до гіпотенузи (прилеглий або протилежний). Вирішив в «довгий ящик не відкладати», необхідний матеріал нижче, прошу ознайомитися 😉
Справа в тому, що я не раз спостерігав, як учні 10-11 класів насилу згадують дані визначення. Вони прекрасно пам’ятають, що катет відноситься до гіпотенузи, а ось який з них — забувають і плутають. Ціна помилки, як ви знаєте на іспиті-це втрачений бал.
Інформація, яку я представлю безпосередньо до математики не має ніякого відношення. Вона пов’язана з образним мисленням, і з прийомами словесно-логічного зв’язку. Саме так, я сам, раз і на завжди запам’ятав дані визначення. Якщо ви їх все ж забудете, то за допомогою представлених прийомів завжди легко згадайте.
Нагадаю визначення синуса і косинуса в прямокутному трикутнику:
Косинус гострого кута в прямокутному трикутнику — це відношення прилеглого катета до гіпотенузи:
Синус гострого кута в прямокутному трикутнику — це відношення протилежного катета до гіпотенузи:
Отже, які асоціації у вас викликає слово косинус?
Напевно, у кожного свої 😉 запам’ятовуйте зв’язку:
Таким чином, у вас відразу в пам’яті виникне вираз–
«… Ставлення прилеглого катета до гіпотенузи» »
Проблема з визначенням косинуса вирішена.
Якщо потрібно згадати визначення синуса в прямокутному трикутнику, то згадавши визначення косинуса, ви без праці встановите, що синус гострого кута в прямокутному трикутнику — це відношення протилежного катета до гіпотенузи. Адже катетів всього два, якщо прилеглий катет «зайнятий» косинусом, то синусу залишається тільки протилежний.
Як бути з тангенсом і котангенсом? плутанина та ж. Учні знають, що це відношення катетів, але проблема згадати який до якого відноситься – чи то протилежний до прилеглого, то чи навпаки.
Визначення:
Тангенс гострого кута в прямокутному трикутнику-це відношення протилежного катета до прилеглого:
Котангенс гострого кута в прямокутному трикутнику — це відношення прилеглого катета до протилежного:
Як запам’ятати? є два способи. Один так само використовує словесно-логічний зв’язок, інший-математичний.
спосіб математичний
Є таке визначення-тангенсом гострого кута називається відношення синуса кута до його косинусу:
*запам’ятавши формулу, ви завжди зможете визначити, що тангенс гострого кута в прямокутному трикутнику — це відношення протилежного катета до прилеглого.
Аналогічно. котангенсом гострого кута називається відношення косинуса кута до його синусу:
Отже! запам’ятавши зазначені формули ви завжди зможете визначити, що:
— тангенс гострого кута в прямокутному трикутнику-це відношення протилежного катета до прилеглого
— котангенс гострого кута в прямокутному трикутнику — це відношення прилеглого катета до протилежного.
спосіб словесно-логічний
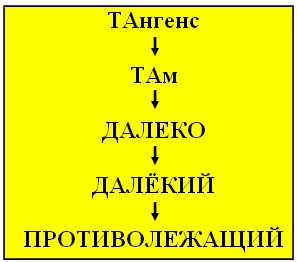
Про тангенсе. Запам’ятайте зв’язку:
Тобто якщо буде потрібно згадати визначення тангенса, за допомогою даної логічної зв’язку, ви без праці згадайте, що це
«… Відношення протилежного катета до прилеглого»
Якщо мова зайде про котангенсе, то згадавши визначення тангенса ви без праці озвучите визначення котангенса–
«… Відношення прилеглого катета до протилежного «
Є цікавий прийом по запам’ятовуванню тангенса і котангенса на сайті» математичний тандем » , подивіться.
спосіб універсальний
Можна просто зазубрити. але як показує практика, завдяки словесно-логічним зв’язкам людина запам’ятовує інформацію надовго, і не тільки математичну.
Сподіваюся, матеріал був вам корисний.
З повагою, олександр крутицьких
P. S: буду вдячний вам, якщо розповісте про сайт в соціальних мережах.
З центром у точці a.
Α-кут, виражений в радіанах.
Визначення
Синус (sin α) — це тригонометрична функція, що залежить від кута α між гіпотенузою і катетом прямокутного трикутника, рівна відношенню довжини протилежного катета |bc| до довжини гіпотенузи |ac|.
Косинус (cos α) — це тригонометрична функція, що залежить від кута α між гіпотенузою і катетом прямокутного трикутника, рівна відношенню довжини прилеглого катета |ab| до довжини гіпотенузи |ac|.
Зміст
Прийняті позначення
;
;
.
;
;
.
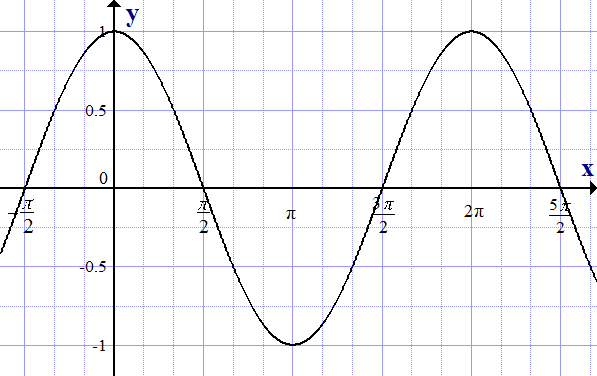
Графік функції синус, y = sin x
Графік функції косинус, y = cos x
Властивості синуса і косинуса
Періодичність
Функції y = sin x і y = cos x періодичні з періодом 2 π .
Парність
Функція синус — непарна. Функція косинус-парна.
Область визначення і значень, екстремуми, зростання, спадання
Функції синус і косинус безперервні на своїй області визначення, тобто для всіх x(див. Їх основні властивості представлені в таблиці (n-ціле).
y = sin x y = cos x область визначення і безперервність — ∞
Основні формули
Сума квадратів синуса і косинуса
Формули синуса і косинуса від суми і різниці
;
;
Формули добутку синусів і косинусів
Формули суми і різниці
Вираз синуса через косинус
;
;
;
.
Вираз косинуса через синус
;
;
;
.
Вираз через тангенс
; .
При, маємо:
; .
При :
; .
Таблиця синусів і косинусів, тангенсів і котангенсів
У даній таблиці представлені значення синусів і косинусів при деяких значеннях аргументу.
Вирази через комплексні змінні
;
Формула ейлера
Вирази через гіперболічні функції
;
;
Похідні
; . висновок формул>>>
Похідні n-го порядку:
{- ∞
Секанс, косеканс
Зворотні функції
Зворотними функціями до синуса і косинусу є арксинус і арккосинус , відповідно.
Арксинус, arcsin
Арккосинус, arccos
Використана література:
І. Н. Бронштейн, к.а. Семендяєв, довідник з математики для інженерів і учнів втузов, «лань», 2009.
Важливі зауваження!
1. Якщо замість формул ти бачиш абракадабру,Почисти кеш. Як це зробити в твоєму браузері написано тут:
2. Перш ніж на почнеш читати статтю, зверни увагу на наш навігатор по найкориснішим ресурсу для
Синус, косинус, тангенс, котангенс
Поняття синуса (), косинуса (), тангенса (), котангенса () нерозривно пов’язані з поняттям кута. Щоб добре розібратися в цих, на перший погляд, складних поняттях (які викликають у багатьох школярів стан жаху), і переконатися, що «не такий страшний чорт, як його малюють», почнемо з самого початку і розберемося в понятті кута.
Поняття кута: радіан, градус
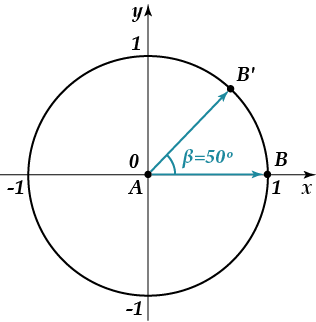
Давай подивимося на малюнку. Вектор» повернувся » щодо точки на якусь величину. Так ось мірою цього повороту щодо початкового положення і буде виступати кут .
Що ж ще необхідно знати про поняття кута? ну, звичайно ж, одиниці виміру кута!
Кут, як в геометрії, так і в тригонометрії, може вимірюватися в градусах і радіанах.
Кутом в (один градус) називають центральний кут в окружності, що спирається на кругову дугу, рівну частині кола. Таким чином, вся окружність складається з» шматочків » кругових дуг, або кут, описуваний колом, дорівнює.
Тобто на малюнку вище зображений кут, рівний, тобто цей кут спирається на кругову дугу розміром довжини кола.
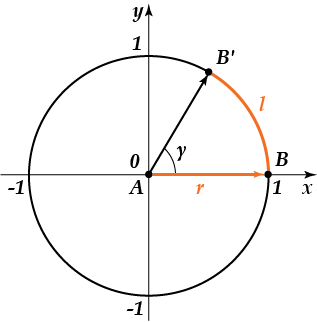
Кутом в радіан називають центральний кут в окружності, що спирається на кругову дугу, довжина якої дорівнює радіусу кола. Ну що, розібрався? якщо ні, то давай розбиратися по малюнку.
Отже, на малюнку зображений кут, рівний радіану, тобто цей кут спирається на кругову дугу, довжина якої дорівнює радіусу кола (довжина дорівнює довжині або радіус дорівнює довжині дуги). Таким чином, довжина дуги обчислюється за формулою:
Де — центральний кут в радіанах.
Ну що, можеш, знаючи це, відповісти, скільки радіан містить кут, описуваний окружністю? так, для цього треба згадати формулу довжини кола. Ось вона:
Ну ось, тепер співвіднесемо ці дві формули і отримаємо, що кут, описуваний окружністю дорівнює. Тобто, співвіднісши величину в градусах і радіанах, отримуємо, що. Відповідно, . Як можна помітити, на відміну від» градусів«, слово» радіан » опускається, так як одиниця виміру зазвичай ясна з контексту.
А скільки радіан складають? все вірно!
Вловив? тоді вперед закріплювати:
Виникли труднощі? тоді дивись відповіді:
Прямокутний трикутник: синус, косинус, тангенс, котангенс кута
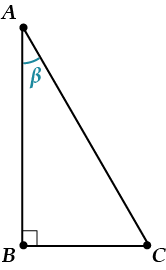
Отже, з поняттям кута розібралися. А що ж все-таки таке синус, косинус, тангенс, котангенс? давай розбиратися. Для цього нам допоможе прямокутний трикутник.
Як називаються сторони прямокутного трикутника? все вірно, гіпотенуза і катети: гіпотенуза — це сторона, яка лежить навпроти прямого кута (у нашому прикладі це сторона); катети — це дві сторони і (ті, що прилягають до прямого кута), причому, якщо розглядати катети щодо кута, то катет — це прилеглий катет, а катет — протилежні. Отже, тепер відповімо на питання: що таке синус, косинус, тангенс і котангенс кута?
Синус кута-це відношення протилежного (далекого) катета до гіпотенузи.
У нашому трикутнику.
Косинус кута — це відношення прилеглого (близького) катета до гіпотенузи.
У нашому трикутнику.
Тангенс кута — це відношення протилежного (далекого) катета до прилеглого (близького).
У нашому трикутнику.
Котангенс кута — це відношення прилеглого (близького) катета до протилежного (далекого).
У нашому трикутнику.
Ці визначення необхідно запам’ятати ! щоб було простіше запам’ятати який катет на що ділити, необхідно чітко усвідомити, що в тангенсе і котангенсе сидять тільки катети, а гіпотенуза з’являється тільки в синусі і косинусі . А далі можна придумати ланцюжок асоціацій. Наприклад, ось таку:
Косинус→торкатися→доторкнутися→прилеглий;
Котангенс→торкатися→доторкнутися→прилеглий.
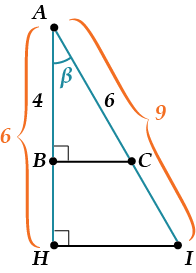
В першу чергу, необхідно запам’ятати, що синус, косинус, тангенс і котангенс як відносини сторін трикутника не залежать від довжин цих сторін (при одному вугіллі). Не віриш? тоді переконайся, подивившись на малюнок:
Розглянемо, наприклад, косинус кута. За визначенням, з трикутника:, але ж ми можемо обчислити косинус кута і з трикутника:. Бачиш, довжини у сторін різні, а значення косинуса одного кута одне і те ж. Таким чином, значення синуса, косинуса, тангенса і котангенса залежать виключно від величини кута.
Якщо розібрався в визначеннях, то вперед закріплювати їх!
Для трикутника, зображеного нижче на малюнку, знайдемо.
Ну що, вловив? тоді пробуй сам: порахуй те ж саме для кута.
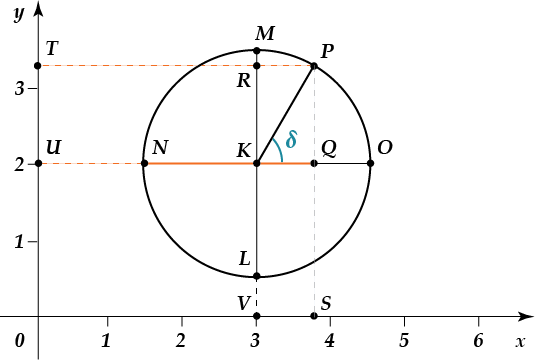
Одинична (тригонометрична) окружність
Розбираючись в поняттях градуса і радіана, ми розглядали коло з радіусом, рівним. Така окружність називається одиничною . Вона дуже стане в нагоді при вивченні тригонометрії. Тому зупинимося на ній трохи детальніше.
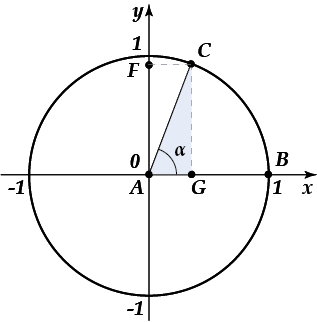
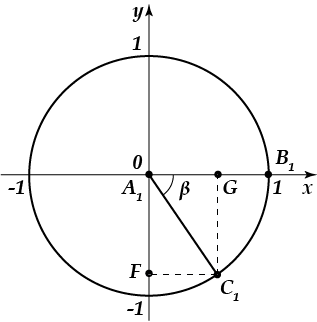
Як можна помітити, дана окружність побудована в декартової системі координат. Радіус кола дорівнює одиниці, при цьому центр кола лежить на початку координат, початкове положення радіус-вектора зафіксовано уздовж позитивного напрямку осі (в нашому прикладі, це радіус).
Кожній точці кола відповідають два числа: координата по осі і координата по осі. А що це за числа-координати? і взагалі, яке відношення вони мають до даної теми? для цього треба згадати про розглянутий прямокутний трикутник. На малюнку, наведеному вище, можна помітити цілих два прямокутних трикутника. Розглянемо трикутник. Він прямокутний, так як є перпендикуляром до осі.
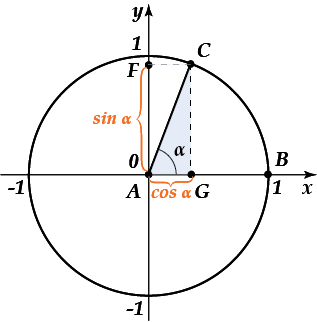
Чому дорівнює з трикутника? все вірно. Крім того, нам адже відомо, що — це радіус одиничного кола, а значить,. Підставимо це значення в нашу формулу для косинуса. Ось що виходить:
А чому дорівнює з трикутника? ну звичайно,! підставимо значення радіуса в цю формулу і отримаємо:
Так, а можеш сказати, які координати має точка, що належить окружності? ну що, ніяк? а якщо збагнути, що і — це просто числа? який координаті відповідає? ну, звичайно, координаті! а який координаті відповідає? все вірно, координаті! таким чином, точка.
А чому тоді рівні і? все вірно, скористаємося відповідними визначеннями тангенса і котангенса і отримаємо, що, а.
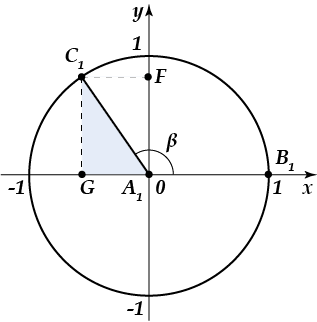
А що, якщо кут буде більше? ось, наприклад, як на цьому малюнку:
Що ж змінилося в даному прикладі? давай розбиратися. Для цього знову звернемося до прямокутного трикутника. Розглянемо прямокутний трикутник: кут (як прилеглий до кута). Чому дорівнює значення синуса, косинуса, тангенса і котангенса для кута? все вірно, дотримуємося відповідних визначень тригонометричних функцій:
Ну ось, як бачиш, значення синуса кута все так же відповідає координаті; значення косинуса кута — координаті; а значення тангенса і котангенса відповідним співвідношенням. Таким чином, ці співвідношення застосовні до будь-яких поворотів радіус-вектора.
Вже згадувалося, що початкове положення радіус-вектора — уздовж позитивного напрямку осі. До цих пір ми обертали цей вектор проти годинникової стрілки, а що буде, якщо повернути його за годинниковою стрілкою? нічого екстраординарного, вийде так само кут певної величини, але тільки він буде негативним. Таким чином, при обертанні радіус-вектора проти годинникової стрілки виходять позитивні кути, а при обертанні за годинниковою стрілкою — негативні.
Отже, ми знаємо, що цілий оборот радіус-вектора по колу становить або. А можна повернути радіус — вектор на або на? ну звичайно, можна! у першому випадку, таким чином, радіус-вектор зробить один повний оборот і зупиниться в положенні або.
У другому випадку, тобто радіус-вектор зробить три повних обороту і зупиниться в положенні або.
Таким чином, з наведених прикладів можемо зробити висновок, що кути, що відрізняються на або (де — будь-яке ціле число), відповідають одному і тому ж положенню радіус-вектора.
Нижче на малюнку зображений кут. Це ж зображення відповідає куту і т.д. Цей список можна продовжити до нескінченності. Всі ці кути можна записати загальною формулою або (де-будь-яке ціле число)
Тепер, знаючи визначення основних тригонометричних функцій і використовуючи одиничну окружність, спробуй відповісти, чому рівні значення:
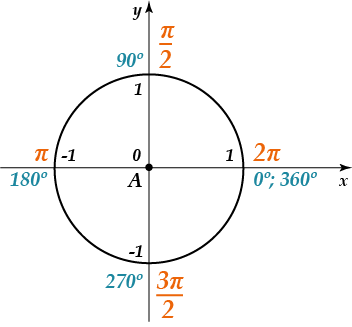
Ось тобі на допомогу одинична окружність:
Виникли труднощі? тоді давай розбиратися. Отже, ми знаємо, що:
Звідси, ми визначаємо координати точок, що відповідають певним заходам кута. Ну що ж, почнемо по порядку: кутку в відповідає точка з координатами,Отже:
Не існує;
Далі, дотримуючись тієї ж логіки, з’ясовуємо, що кутам в відповідають точки з координатами, відповідно. Знаючи це, легко визначити значення тригонометричних функцій у відповідних точках. Спочатку спробуй сам, а потім звіряйся з відповідями.
Відповіді:
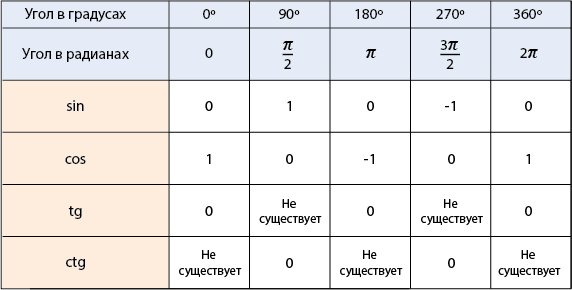
Таким чином, ми можемо скласти наступну табличку:
Немає необхідності пам’ятати всі ці значення. Досить пам’ятати відповідність координат точок на одиничній окружності і значень тригонометричних функцій:
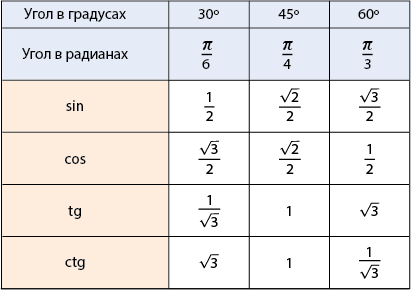
А ось значення тригонометричних функцій кутів в і, наведених нижче в таблиці, необхідно запам’ятати :
Не треба лякатися, зараз покажемо один із прикладів досить простого запам’ятовування відповідних значень:
Для користування цим методом життєво необхідно запам’ятати значення синуса для всіх трьох заходів кута (), а також значення тангенса кута в. Знаючи ці значення, досить просто відновити всю таблицю цілком-значення косинуса переносяться відповідно до стрілочками, тобто:
Знаючи це можна відновити значення для. Чисельник « » відповідатиме, а знаменник «» відповідає. Значення котангенса переносяться відповідно до стрілочками, зазначеними на малюнку. Якщо це усвідомити і запам’ятати схему зі стрілочками, то буде досить пам’ятати всього значення з таблиці.
Координати точки на окружності
А чи можна знайти точку (її координати) на окружності, знаючи координати центру кола, її радіус і кут повороту ?
Ну, звичайно, можна! давай виведемо загальну формулу для знаходження координат точки .
Ось, наприклад, перед нами таке коло:
Нам дано, що точка-центр кола. Радіус кола дорівнює. Необхідно знайти координати точки, отриманої поворотом точки на градусів.
Як видно з малюнка, координаті точки відповідає довжина відрізка. Довжина відрізка відповідає координаті центру кола, тобто дорівнює. Довжину відрізка можна виразити, використовуючи визначення косинуса:
Тоді маємо, що для точки координата.
За тією ж логікою знаходимо значення координати y для точки. Таким чином,
Отже, в загальному вигляді координати точок визначаються за формулами:
Координати центру кола,
Радіус кола,
Кут повороту радіуса вектора.
Як можна помітити, для розглянутої нами одиничної окружності ці формули значно скорочуються, так як координати центру дорівнюють нулю, а радіус дорівнює одиниці:
Ну що, спробуємо ці формули на смак, повправляючись в знаходженні точок на колі?
1. Знайти координати точки на одиничній окружності, отриманої поворотом точки на.
2. Знайти координати точки на одиничній окружності, отриманої поворотом точки на.
3. Знайти координати точки на одиничній окружності, отриманої поворотом точки на.
4. Точка-центр кола. Радіус кола дорівнює. Необхідно знайти координати точки, отриманої поворотом початкового радіус-вектора на.
5. Точка-центр кола. Радіус кола дорівнює. Необхідно знайти координати точки, отриманої поворотом початкового радіус-вектора на.
Виникли проблеми в знаходженні координат точки на колі?
Виріши ці п’ять прикладів (або розберися добре в рішенні) і ти навчишся їх знаходити!
Короткий виклад і основні формули
Синус кута — це відношення протилежного (далекого) катета до гіпотенузи.
Косинус кута — це відношення прилеглого (близького) катета до гіпотенузи.
Тангенс кута — це відношення протилежного (далекого) катета до прилеглого (близького).
Котангенс кута — це відношення прилеглого (близького) катета до протилежного (далекого).
Ну ось, тема закінчена. Якщо ти читаєш ці рядки, значить ти дуже крутий.
Тому що тільки 5% людей здатні освоїти щось самостійно. І якщо ти дочитав до кінця, значить ти потрапив в ці 5%!
Тепер найголовніше.
Ти розібрався з теорією по цій темі. І, повторюся, це … Це просто супер! ти вже краще, ніж абсолютна більшість твоїх однолітків.
Проблема в тому, що цього може не вистачити…
Для чого?
Для успішної здачі єді, для вступу до інституту на бюджет і, найголовніше, для життя.
Я не буду тебе ні в чому переконувати, просто скажу одну річ…
Люди, які отримали гарну освіту, заробляють набагато більше, ніж ті, хто його не отримав. Це статистика.
Але і це-не головне.
Головне те, що вони більш щасливі (є такі дослідження). Можливо тому, що перед ними відкривається набагато більше можливостей і життя стає яскравішим? не знаю…
Але, думай сам…
Що потрібно, щоб бути напевно краще за інших на єді і бути в кінцевому підсумку … Більш щасливим?
Набити руку, вирішуючи завдання по цій темі.
На іспиті у тебе не будуть питати теорію.
Тобі потрібно буде вирішувати завдання на час .
І, якщо ти не вирішував їх (багато!), ти обов’язково де-небудь нерозумно помилишся або просто не встигнеш.
Це як у спорті — потрібно багато разів повторити, щоб виграти напевно.
Знайди де хочеш збірник, обов’язково з рішеннями, докладним розбором і вирішуй, вирішуй, вирішуй!
Можна скористатися нашими завданнями (не обов’язково) і ми їх, звичайно, рекомендуємо.
Для того, щоб набити руку за допомогою наших завдань потрібно допомогти продовжити життя підручнику youclever, який ти зараз читаєш.
Як? є два варіанти:
- відкрий доступ до всіх прихованих завдань в цій статті-
- відкрий доступ до всіх прихованих завдань у всіх 99-ти статтях підручника-купити підручник-499 руб
Так, у нас в підручнику 99 таких статей і доступ для всіх завдань і всіх прихованих текстів в них можна відкрити відразу.
Доступ до всіх прихованих завдань надається на весь час існування сайту.
І на закінчення…
Якщо наші завдання тобі не подобаються, знайди інші. Тільки не зупиняйся на теорії.
«зрозумів» і «вмію вирішувати» — це абсолютно різні навички. Тобі потрібні обидва.
Знайди завдання і вирішуй!
– вже напевно зустрінуться завдання з тригонометрії. Тригонометрію часто не люблять за необхідність зубрити величезну кількість важких формул, що кишать синусами, косинусами, тангенсами і котангенсами. На сайті вже колись давалися поради, як згадати забуту формулу, на прикладі формул ейлера і піля .
А в цій статті ми постараємося показати, що досить твердо знати всього п’ять найпростіших тригонометричних формул, а про інших мати загальне уявлення і виводити їх по ходу справи. Це як з днк: в молекулі не зберігаються повні креслення готового живої істоти. Там містяться, скоріше, інструкції по його збірці з наявних амінокислот. Так і в тригонометрії, знаючи деякі загальні принципи, ми отримаємо всі необхідні формули з невеликого набору тих, які потрібно обов’язково тримати в голові.
Будемо спиратися на наступні формули:
З формул синуса і косинуса сум, знаючи про парність функції косинуса і про непарність функції синуса ,підставивши-b замість b, отримуємо формули для різниць:
- синус різниці: sin (a-b) = sin a cos (- b) + cos a sin (- b) = sin a cos b-cos a sin b
- косинус різниці: cos (a-b) = cos a cos (- b) -sin a sin (- b) = cos a cos b +sin a sin b
Поставляючи в ці ж формули a = b, отримуємо формули синуса і косинуса подвійних кутів:
- синус подвійного кута : sin 2a = sin (a+a) = sin a cos a +cos a sin a = 2sin a cos a
- косинус подвійного кута: cos 2a = cos (a+a) = cos a cos a-sin a sin a = cos 2 a-sin 2 a
Аналогічно виходять і формули інших кратних кутів:
- синус потрійного кута : sin 3a = sin (2a+a) = sin 2a cos a +cos 2a sin a = (2sin a cos a )cos a +(cos 2 a-sin 2 a )sin a = 2sin a cos 2 a +sin a cos 2 a-sin 3 a = 3sin a cos 2 a-sin 3 a = 3sin a (1-sin 2 a )-sin 3 a = 3sin a-4sin 3 a
- косинус потрійного кута : cos 3a = cos (2a+a) = cos 2a cos a-sin 2a sin a = (cos 2 a-sin 2 a) cos a -(2sin a cos a )sin a = cos 3 a-sin 2 a cos a-2sin 2 a cos a = cos 3 a-3sin 2 a cos a = cos 3 a-3 (1-cos 2 a )cos a = 4cos 3 a-3cos a
Перш ніж рухатися далі, розглянемо одне завдання.
Дано: кут-гострий.
Знайти його косинус, якщо
Рішення, дане одним учнем:
Оскільки, то sin a = 3, а cos a = 4.
(з математичного гумору)
Отже, визначення тангенса пов’язує цю функцію і з синусом, і з косинусом. Але можна отримати формулу, що дає зв’язок тангенса тільки з косинусом. Для її виведення візьмемо основне тригонометричне тотожність: sin 2 a +cos 2 a = 1 і розділимо його на cos 2 a . Отримаємо:
Так що вирішенням цього завдання буде:
(тому що кут гострий, при витяганні кореня береться знак +)
Формула тангенса суми-ще одна, важко піддається запам’ятовуванню. Виведемо її так:
Відразу виводиться і
З формули косинуса подвійного кута можна отримати формули синуса і косинуса для половинного. Для цього до лівої частиниФормули косинуса подвійного кута:
Cos 2 a = cos 2 a -sin 2 a
Додаємо одиницю, а до правої – тригонометричну одиницю, тобто суму квадратів синуса і косинуса.
Cos 2a +1 = cos 2 a -sin 2 a +cos 2 a +sin 2 a
2cos 2 a = cos 2 a +1
Висловлюючи cos a через cos 2 a і виконуючи заміну змінних, отримуємо:
Знак береться в залежності від квадранта.
Аналогічно, віднявши від лівої частини рівності одиницю, а від правої-суму квадратів синуса і косинуса, отримаємо:
Cos 2a -1 = cos 2 a -sin 2 a -cos 2 a -sin 2 a
2sin 2 a = 1-cos 2 a
І, нарешті, щоб перетворити суму тригонометричних функцій у добуток, використовуємо наступний прийом. Припустимо, нам потрібно представити у вигляді твору суму синусів sin a + sin b . Введемо змінні x і y такі, що a = x + y, b + x-y. Тоді
Sin a + sin b = sin(x + y) + sin (x-y) = sin xcos y + cos xsin y+sin xcos y-cos xsin y = 2sin xcos y. Висловимо тепер x і y через a і b.
Оскільки a = x+y, b = x-y, то . Тому
Відразу ж можна вивести
- формулу для розбиття добутку синуса і косинуса в суму: sin a cos b = 0.5 (sin (a+b) +sin (a-b))
Рекомендуємо потренуватися і вивести самостійно формули для перетворення в добуток різниці синусів і суми і різниці косинусів, а також для розбиття в суму добутків синусів і косинусів. Виконавши ці вправи, ви досконально освоїте майстерність виведення тригонометричних формул і не загубитеся навіть на найскладнішій контрольній, олімпіаді або тестуванні.